Posted by Edd Mann on Jul 22, 2015
Insertion, Removal and Inversion Operations on Binary (Search) Trees in PHP
Recently Max Howell (creator of Homebrew) posted an interesting tweet in regard to Google’s interview process. In this tweet he mentioned how one of the proposed questions was to white-board a solution to invert a binary tree. Over the past couple of years I have been interested in exploring fundamental Computer Science data-structures and algorithms. As a result, I thought it would be interesting to explore this structure and associated operations in more depth - using immutable and mutable PHP implementations to clearly highlight the benefits garnered from each approach.
Binary trees are a form of tree data-structure, comprised of nodes with assigned values and at-most two child nodes (left and right). To expand on this problem I will be documenting the creation of an Binary Search Tree, which has the additional invariant that any left child be less than, and any right child be greater than, the current nodes value. This allows us to perform unambiguous node deletion from the structure.
Node Representation
Throughout all these examples I leaned towards a simple function, as opposed to class-based approach, relying on namespaces to infer relation. The following function can be used to create a simple object representation of a tree node. Providing a value and optional left and right nodes, it simply returns the aggregate.
function Node($value, $left = null, $right = null)
{
return (object) compact('value', 'left', 'right');
}
Insertion
Now that we are able to represent tree nodes, the next logical step is to provide insertion capabilities. Accessible from the root tree node (initially NULL), we are able to recursively traverse the structure until we either find a leaf or the node already present. To decide which child to traverse down we use the discussed comparator invariant. Below is a small diagram depicting the insertion of a value within an existing tree.
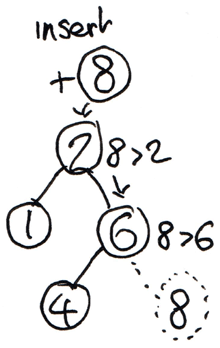
Mutable
The first implementation provides a mutable means of insertion. Notice the explicit reassignment of the right and left child node references.
function insert($value, $root)
{
if ($root === null) {
return Node($value);
}
if ($value === $root->value) {
return $root;
}
if ($value > $root->value) {
$root->right = insert($value, $root->right);
} else {
$root->left = insert($value, $root->left);
}
return $root;
}
Immutable
Below is an immutable implementation of the insertion process starting from a rooted tree node. As opposed to modifying pre-existing state, we instead build up a modified representation, creating new nodes when required. This allows us to the use both the new and old tree representations simultaneously.
function insert($value, $root)
{
if ($root === null) {
return Node($value);
}
if ($value === $root->value) {
return $root;
}
if ($value > $root->value) {
return Node($root->value, $root->left, insert($value, $root->right));
}
return Node($root->value, insert($value, $root->left), $root->right);
}
Removal
With the ability to now insert nodes into the tree, we can expand on this by performing the inverse operation, that being removal. When removing a node from the tree, there are three different use-cases that need to be addressed. The first two are relativity simple cases, met when the node in question has zero or one child. When no children are present we are able to just remove the reference to the node. However, in the case of a single child node we can replace the nodes parent reference with its child node. The third case is a little more tricky, requiring us to rearrange the structure to find a new node to replace this one, maintaining the desired invariant.
There are two common techniques to achieve this, either finding the in-order successor or in-order predecessor and replacing the current node with this result. In these examples I have opted for the in-order successor, which requires us to find the minimal value of the current nodes right tree. This operation can be succinctly codified recursively as shown below.
function minValue($root)
{
if ($root->left === null) {
return $root->value;
}
return minValue($root->left);
}
Below is a small diagram depicting the removal of a node which meets the third use-case.
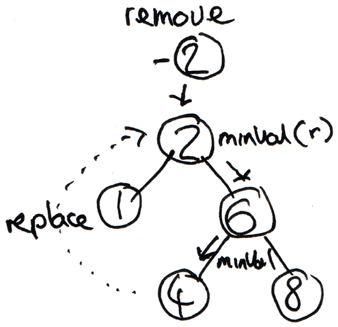
Mutable
In a similar fashion to how mutable insertion can be carried out, we reassign both the nodes right and left references when required. We also replace the current nodes value, if the operation falls into the described third use-case.
function remove($value, $root)
{
if ($root === null) {
return $root;
}
if ($value > $root->value) {
$root->right = remove($value, $root->right);
return $root;
}
if ($value < $root->value) {
$root->left = remove($value, $root->left);
return $root;
}
if ($root->right === null) {
return $root->left;
}
if ($root->left === null) {
return $root->right;
}
$value = minValue($root->right);
$root->right = remove($value, $root->right);
$root->value = $value;
return $root;
}
Immutable
In the immutable instance we instead return new nodes in place of the reassignment that would have occurred in the mutable version. This allows us to maintain and access the entire original tree structure, whilst reusing unmodified references in the new tree.
function remove($value, $root)
{
if ($root === null) {
return $root;
}
if ($value > $root->value) {
return Node($root->value, $root->left, remove($value, $root->right));
}
if ($value < $root->value) {
return Node($root->value, remove($value, $root->left), $root->right);
}
if ($root->left === null) {
return $root->right;
}
if ($root->right === null) {
return $root->left;
}
$value = minValue($root->right);
return Node($value, $root->left, remove($value, $root->right));
}
Inversion
Now that we have the ability to insert and remove nodes from a binary tree, another operation which can be performed is inversion (like the tweet mentioned). I should note that this operation does not typically occur on Binary Search Trees as it violates the additional invariant.
Mutable
From a mutable perspective we are able to invert the tree in a memory efficient manner, with only references being altered.
function invert($root)
{
if ($root === null) {
return $root;
}
$tmp = $root->left;
$root->left = invert($root->right);
$root->right = invert($tmp);
return $root;
}
Immutable
In the case of immutability, an entirely new tree is required to be built. As to maintain the ability to reuse the current tree we are not able to manipulate any of the existing nodes references.
function invert($root)
{
if ($root === null) {
return $root;
}
return Node($root->value, invert($root->right), invert($root->left));
}
Example
Now that we have these operations in place we can use the following function to generate a tree from an array representation. Notice the use of the mutable insert operation to save on memory costs.
function fromArray(array $values)
{
$tree = null;
foreach ($values as $value) {
$tree = BinaryTree\Mutable\insert($value, $tree);
}
return $tree;
}
We can then visualise the generated tree by using the following render function. This function displays the tree from left to right, as opposed to the typical top down approach.
function render($root, $depth = 0)
{
if ($root === null) {
return str_repeat("\t", $depth) . "~\n";
}
return
render($root->right, $depth + 1) .
str_repeat("\t", $depth) . $root->value . "\n" .
render($root->left, $depth + 1);
}
Finally, we are able to use all these operations and helper functions in conjunction, for a contrived example.
$a = BinaryTree\fromArray([ 2, 1, 3, 4 ]);
$b = BinaryTree\Immutable\remove(2, $a);
echo BinaryTree\render($a);
/*
~
4
~
3
~
2
~
1
~
*/
BinaryTree\Mutable\invert($b);
echo BinaryTree\render($b);
/*
~
1
~
3
~
4
~
*/

